- The Language Of Physics Is Mathematics-


Friday, 13 July 2012

LINEAR GRAPHS


Relations

In mathematics, we use symbols to denote relations and we build mathematical sentences using numbers, pronumerals and relations.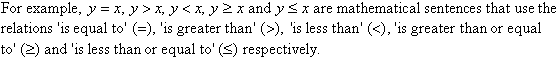For example, y = x, y > x, y < x, y >= x, y <= x are mathematical sentences that use the relation 'is equal to' (=), 'is greater than' (>), 'is less than' (<), 'is greater than or equal to' (>=) and 'is less than or equal to' (<=) respectively.
Consider the following sentence:
The cost (in dollars) of buying pens is equal to ten times the number of pens bought.
If c represents the cost in dollars and p represents the number of pens bought, then this sentence can be expressed mathematically as

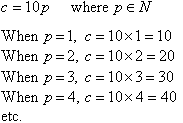
c = 10p where p is an element of N. When p = 1, c = 10. When p = 2, c = 20. When p = 3, c = 30. When p = 4, c = 40 etc.
Thus the mathematical sentence c = 10p relates the values of c to the values of p. It defines a binary relation on the natural numbers.
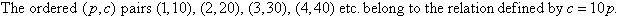
The ordered (p, c) pairs (1, 10), (2, 20), (3, 30), (4, 40) etc. belong to the relation defined by c = 10p.

This suggests the following definition:
A relation is a set of ordered pairs, and is usually defined by a rule.
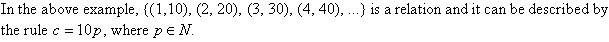
In the above example, {(1, 10), (2, 20), (3, 30), (4, 40), ...} is a relation and it can be described by the rule c = 10p, where p is an element of N.

Domain

The domain of a relation is the set of all first elements (usually x values) of its ordered pairs.
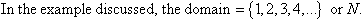
In the example discussed, the domain = {1,2,3,4,...} or N.

Range

The range of a relation is the set of all second elements (usually y values) of its ordered pairs.
In the example discussed, the range = {10,20,30,40,...}.
Note:
The graph of c against p is discrete because p is an element of the set of natural numbers. The values of c depend upon p. So, we say that p is anindependent variable and c is a dependent variable.


Example 1

State the domain and range of the following relations:
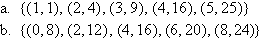
(a) {(1,1), (2,4), (3,9), (4,16), (5,25)} (b) {(0,8), (2,12), (4,16), (6,20), (8,24)}
Solution:
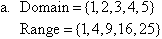
(a) Domain = {1,2,3,4,5}, Range = (1,4,9,16,25}
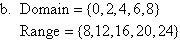
(b) Domain = {0,2,4,6,8}, Range = (8,12,16,20,24}


Functions

A relation is said to be a function if each element of the domain determines exactly one element of the range.
For example, the relation c = 10p, where p is an element of N, is a function since each element of the domain determines exactly one element of the range.

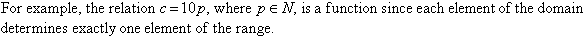
Domain of a Function

The domain of a function is the set of all first elements (usually x values) of its ordered pairs.
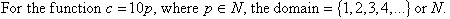
For the function, c = 10p, where p is an element of N, the domain = {1,2,3,4,...} or N.

Range of a Function

The range of a function is the set of all second elements (usually y values) of its ordered pairs.
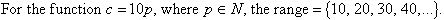
For the function, c = 10p, where p is an element of N, the range = {10,20,30,40,...}.


Example 2

State the domain and range of the following functions:

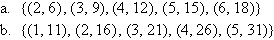
(a) {(2,6), (3,9), (4,12), (5,15), (6,18)} (b) {(1,11), (2,16), (3,21), (4,26), (5,31)}
Solution:
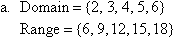
(a) Domain = {2,3,4,5,6}, Range = (6,9,12,15,18}
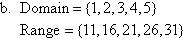
(b) Domain = {1,2,3,4,5}, Range = (11,16,21,26,31}


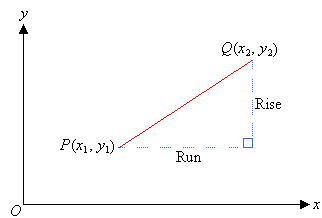
Gradient of a Straight Line

The gradient of a straight line is the rate at which the line rises (or falls) vertically for every unit across to the right.
 That is:

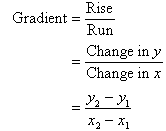
Gradient = Rise / Run = Change in y / Change in x = (y2 - y1) / (x2 - x1)

A linear graph on the Cartesian plane shows the line PQ defined by the point P(x1, y1) and Q(x2, y2). The rise and run between the two points is shown.
Note:
The gradient of a straight line is denoted by m where:
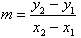
m = (y2 - y1) / (x2 - x1)


Example 3

Find the gradient of the straight line joining the points P(– 4, 5) and Q(4, 17).

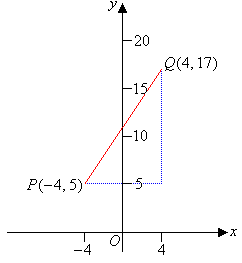
The points P(-4, 5) and Q(4, 17) form a straight line on the Cartesian plane.
Solution:
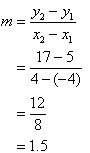
m = (y2 - y1) / (x2 - x1) = (17 - 5) / (4 - (-4)) = 12 / 8 = 1.5


So, the gradient of the line PQ is 1.5.


Note:
If the gradient of a line is positive, then the line slopes upward as the value of x increases.


Example 4

Find the gradient of the straight line joining the points A(6, 0) and B(0, 3).

Solution:
Let (x1, y1) = (6, 0) and (x2, y2) = (0, 3).

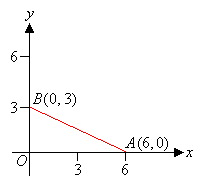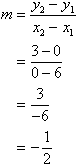The points A(6,0) and B(0,3) form a straight line on the Cartesian plane.m = (y2 - y1) / (x2 - x1) = (3 - 0) / (0 - 6) = 3 / -6 = - 1/2So, the gradient of the line AB is - 1/2.



Note:
If the gradient of a line is negative, then the line slopes downward as the value of x increases.


Applications of Gradients

Gradients are an important part of life. The roof of a house is built with a gradient to enable rain water to run down the roof. An aeroplane ascends at a particular gradient after take off, flies at a different gradient and descends at another gradient to safely land. Tennis courts, roads, football and cricket grounds are made with a gradient to assist drainage.

Example 5

A horse gallops for 20 minutes and covers a distance of 15 km, as shown in the diagram.
Find the gradient of the line and describe its meaning.

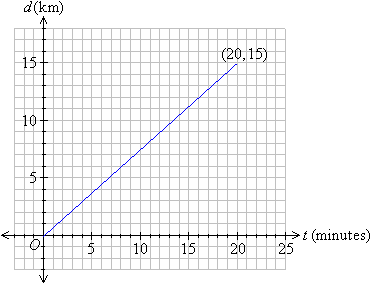
The graph of distance, d, in km against time, t, in minutes depicts the horse's journey from the point (0,0) to the point (20,15).
Solution:
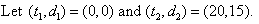
Let (t1, d1) = (0,0) and (t2, d2) = (20,15).

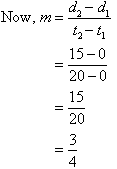
Now, m = (d2 - d1) / (t2 - t1) = (15 - 0) / (20 - 0) = 15 / 20 = 3 / 4
So, the gradient of the line is 3 / 4 km/min.In the above example, we notice that the gradient of the distance-time graph gives the speed (in kilometres per minute); and the distance covered by the horse can be represented by the equation:

d = 3/4t {Because distance = speed * time}


Example 6

The cost of transporting documents by courier is given by the line segment drawn in the diagram. Find the gradient of the line segment; and describe its meaning.

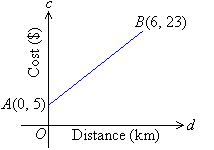
The graph of cost($), c, against distance, d, in km shows the points A(0,5) and B(6,23) forming a straight line.
Solution:
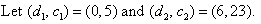
Let (d1,c1) = (0,5) and (d2,c2) = (6,23).

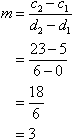
m = (c2 - c1) / (d2 - d1) = (23 - 5) / (6 - 0) = 18 / 6 = 3             
So, the gradient of the line is 3. This means that the cost of transporting documents is $3 per km plus a fixed charge of $5, i.e. it costs $5 for the courier to arrive and $3 for every kilometre travelled to deliver the documents.


Equation of a Straight Line

To establish a rule for the equation of a straight line, consider the previous example.An increase in distance by 1 km results in an increase in cost of $3. We say that the rate of change of cost with respect to distance is $3 per kilometre.
The information given in the graph can be represented by the equation c = 5 + 3d.  That is:

c = 3d + 5 where the gradient of the line = coefficient of d = 3 and the vertical axis intercept = 5


In general:
A line with equation y = mx + c has gradient m and y-intercept c.
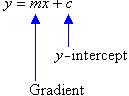
y = mx + c where m is the gradient and c is the y-intercept
The gradient of a straight line is the coefficient of x.

Particular Case
If a straight line passes through the origin, then its y-intercept is 0.  So, the equation of a straight line passing through the origin is
y = mx
where m is the gradient of the line.
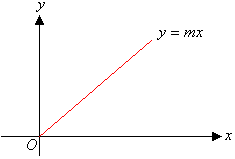
The graph of y = mx which passes through the origin at (0,0).


Example 7

Write down the gradient and the y-intercept for the following equations: (a) y = 4x + 3 (b) 6x + 3y = 9
Solution:
(a) Comparing y = 4x + 3 with y = mx + c gives m = 4, c = 3. So, the gradient is 4 and the y-intercept is 3.          
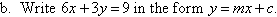
(b) Write 6x + 3y = 9 in the form y = mx + c
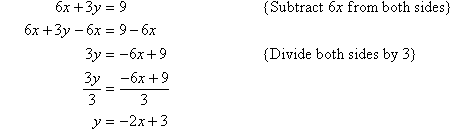
Subtract 6x from both sides and then divide both sides by 3 to find y = -2x + 3.
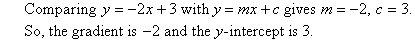
Comparing y = -2x + 3 with y = mx + c gives m = -2, c = 3. So, the gradient is -2 and the y-intercept is 3.


Example 8

Write down the equation of the straight line that has m = 5 and c = 3.
Solution:
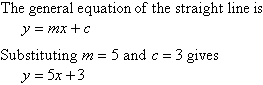
The general equation of the straight line is y = mx + c. Substituting m = 5 and c = 3 gives y = 5x + 3.                 


Example 9

Calculate the gradient of the straight line given in the following diagram; and find its equation.
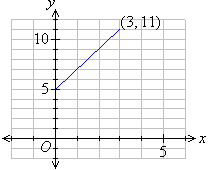
The graph of the straight line joined by the points (0,5) and (3,11).

Solution:
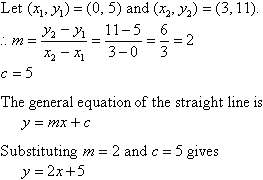
Let (x1, y1) = (0, 5) and (x2, y2) = (3, 11). m = (y2 - y1) / (x2 - x1) = (11 - 5) / (3 - 0) = 6 / 3 = 2 and c = 5. The general equation of the straight line is y = mx + c. Substituting m = 2 and c = 5 gives y = 2x + 5.


Example 10

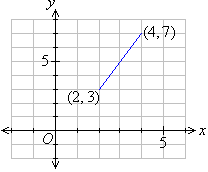
Find the equation of the line joining the points (2, 3) and (4,7).
Solution:
The graph of the straight line joined by the points (2,3) and (4,7).


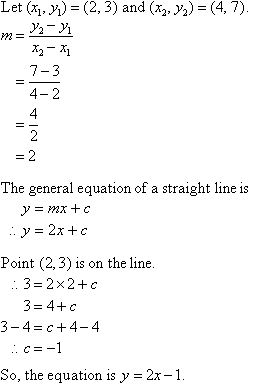
Let (x1, y1) = (2,3) and (x2, y2) = (4, 7). m = (y2 - y1) / (x2 - x1) = (7 - 3) / (4 - 2) = 4 / 2 = 2. The general equation of a straight line is y = mx + c. Therefore, y = 2x + c. Using point (2,3) which is on the line in y = 2x + c gives c = -1. So, the equation is y = 2x - 1.





Sketch Graphs

Often we need to know the general shape and location of a graph.  In such cases, a sketch graph is drawn instead of plotting a number of points to obtain the graph.Two points are needed to obtain a straight line graph.  It is simpler to find the points of intersection of the graph with the axes.  These points are called thex- and y- intercepts.
x-intercept:
The y-coordinate of any point on the x-axis is 0.  Therefore to find the x-intercept we put y = 0 in the equation and solve it for x.
y-intercept:
The x-coordinate of any point on the y-axis is 0.  Therefore to find the y-intercept we put x = 0 in the equation and solve it for y.
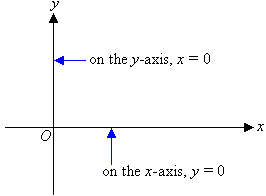The graph shows x = 0 on the y-axis and y = 0 on the x-axis.

 

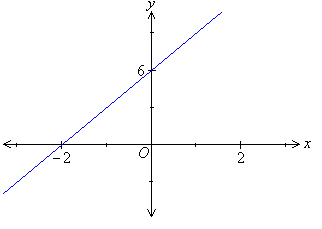
Example 11

Sketch the graph of y = 3x + 6.
Solution:
 y = 3x + 6x-intercept:
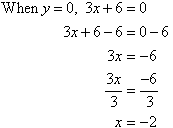
The sketch graph on the Cartesian plane that goes through (-2, 0) and (0, 6).When y = 0, x = -2
 y-intercept:

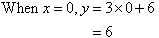When x = 0, y = 6



Note:
We often represent the gradient and the y-intercept of the straight line by m and c respectively.

In the previous example:   


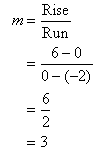
m = Rise / Run = (6 - 0) / (0 - (-2)) = 6 / 2 = 3


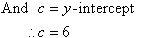
And c = y-intercept = 6


From the ongoing discussion we can infer that y = 3x + 6 is a straight line with a gradient of 3 and y-intercept of 6.
In the example under consideration, the gradient of the straight line is positive.  So, the straight line slopes upward as the value of x increases.

Example 12

Sketch the graph of  y = –2x + 4.
Solution:
 y = –2x + 4

x-intercept:
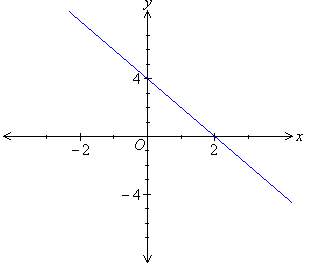
The sketch graph of the line that passes through the points (2, 0) and (0, 4).
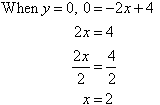
When y = 0, x = 2

 y-intercept:

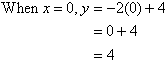When x = 0, y = 4


Note:
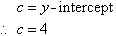
c = y-intercept = 4
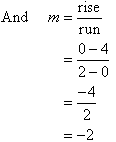
And m = rise/run = (0 - 4) / (2 - 0) = -4 / 2 = -2

From the ongoing discussion we find that the linear function y = –2x + 4 represents the equation of a straight line with a gradient of –2 and y-intercept of 4.

In the example under consideration, the gradient of the straight line is negative. So, the straight line slopes downward as the value of x increases.


Example 13

Sketch the graph of  y = 2x.
Solution:
 y = 2xx-intercept:
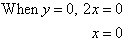
When y = 0, x = 0
 y-intercept:
The graph of y = 2x passes through the origin at (0, 0).

When x = 0, y = 0.
As both the x- and y- intercepts are (0, 0), another point is needed.
We find when x = 5, y = 10.  So, (5, 10) is an example of another point that can be used to form the straight line graph.
Alternative technique:
Use the gradient-intercept method:

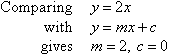
Comparing y = 2x with y = mx + c gives m = 2, c = 0.


The sketch graph of 7y - 5x = 35 that has an x-intercept of -7 and a y-intercept of 5.

So, the straight line passes through (0, 0).  Use this point to draw a line of slope 2 (i.e. go across 3 units and up 6 units).

The graph of y = 2x that highlights a rise of 6 for every run of 3.
Note:
It is simpler to find the run and rise if we start from the y-intercept.


Example 14

Sketch the graph of 7y – 5x = 35.
Solution:
7y – 5x = 35
x-intercept:
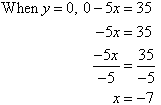
When y = 0, x = -7
 y-intercept:
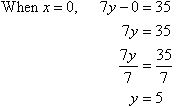
When x = 0, y = 5


Horizontal Lines

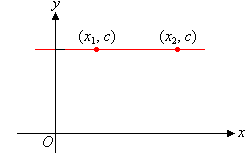
A horizontal line is parallel to the x-axis, as shown in the following diagram.

A graph with a horizontal line that is parallel to the x-axis.
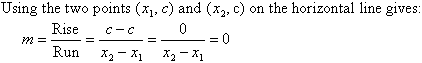
Using the two points (x1, c) and (x2, c) on the horizontal line to calculate the gradient, m, we find that m = 0.

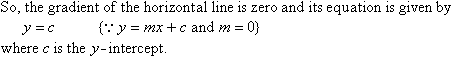
So, the gradient of the horizontal line is zero and its equation is given by y = c where c is the y-intercept.


Note:
The value of the y-coordinate on a horizontal line is always equal to c, the y-intercept.


Example 15

Sketch the graph of y = 8.
Solution:
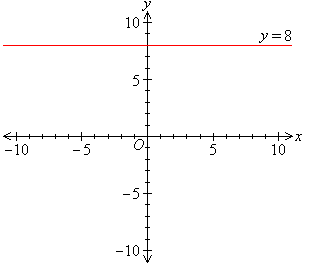
The linear graph of y = 8 is a horizontal line parallel to the x-axis that cuts the y-axis at y = 8. 

Vertical Lines

A vertical line is parallel to the y-axis, as shown in the following diagram.

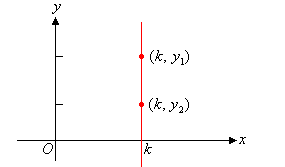
The graph shows a vertical line that is parallel to the y-axis.


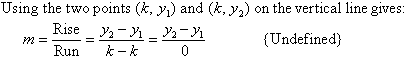
Using the two points (k, y1) and (k, y2) on the vertical line to calculate the gradient, m, we find the gradient is undefined.

So, the gradient of the vertical line is undefined and its equation is given by x = k where k is the x-intercept.

Note:
The value of the x-coordinate on a vertical line is always equal to k, the x-intercept.


Example 16

Sketch the graph of x = 8.
Solution:
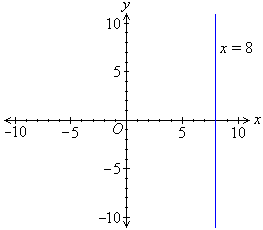The graph shows the vertical line of x = 8 that is parallel to the y-axis and cuts the x-axis at x = 8.




Labels:

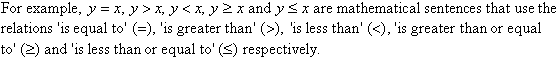
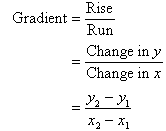
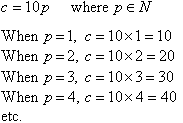
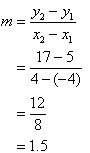
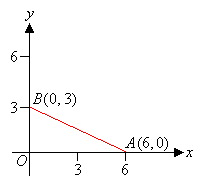
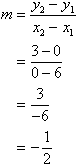
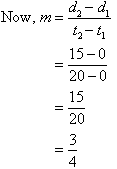
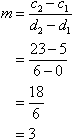
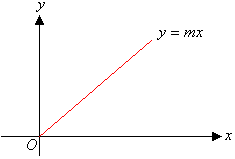
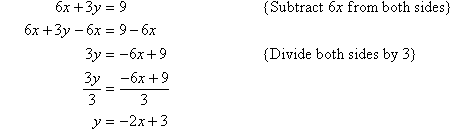
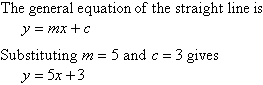
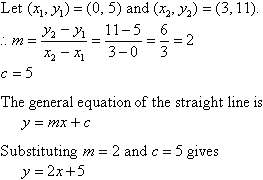
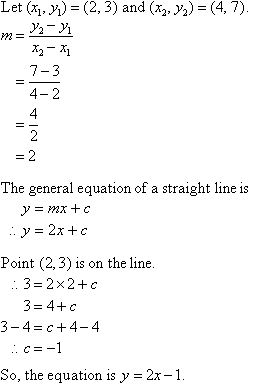
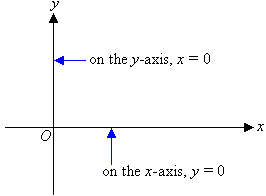
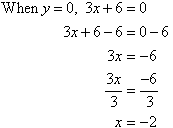
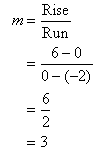
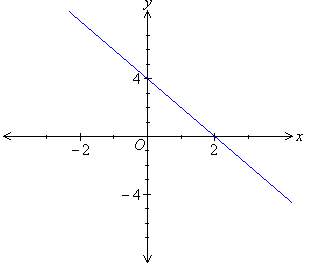
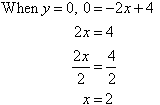
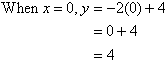
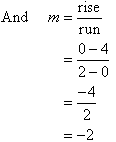
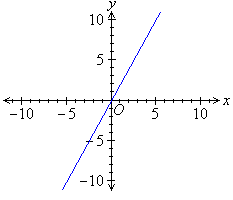
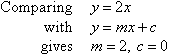
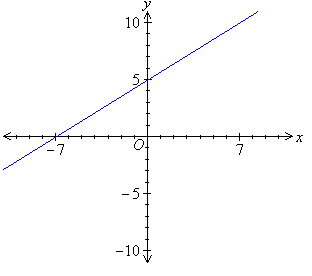
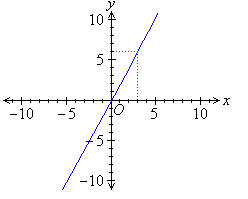
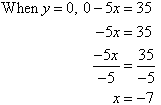
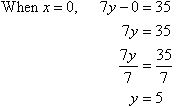
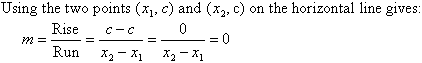
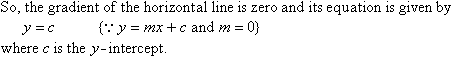
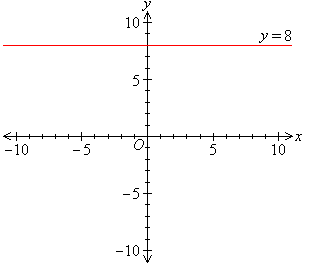
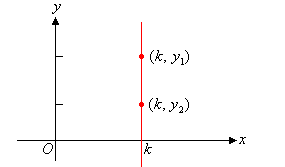
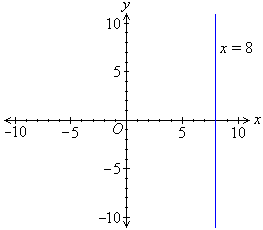
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)